牛顿迭代法

牛顿迭代法是求解一元非线性方程根的方法中非常重要、且比较快速的一种。它把f(x)作一阶泰勒级数展开，将非线性方程的求根问题转化为求解一系列线性方程的根。

牛顿迭代法的迭代公式如下：

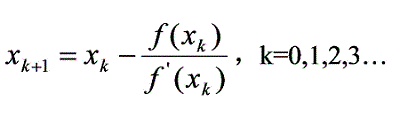
牛顿迭代法的基本步骤如下：

#include <stdio.h>
#include <math.h>
#define eps 0.00001 /* 容许误差*/
float f(float x) /* 定义函数f(x) */
{
return pow(x,3)+2*x+40-exp(x);
}
float f1(float x) /* 定义函数f(x)的导数*/
{
return 3*pow(x,2)+2-exp(x);
}
main()
{
float x0,x1;
int N=0;/*统计迭代次数*/
printf("Please input x0:\n");
scanf("%f",&x0);/*输入初始值x0*/
do
{
N++;
x1=x0-f(x0)/f1(x0); /* 牛顿迭代*/
x0=x1; /* 准备下一次迭代的初值*/
}while(fabs(x1-x0)>eps || fabs(f(x1))>eps ); /*满足精度,输出近似根*/
printf("x=%f, NO.=%d\n",x1,N);
system("pause");
}